順序尺度の場合のアンケート分析①と順序尺度の場合のアンケート分析②では、定食Aの満足度に関するアンケート結果に関して、ダミー変数を用いて重回帰分析を行うことによって、以下の回帰式が得られることを解説しました。
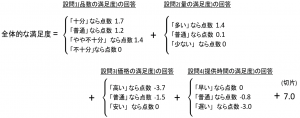
しかしながら、この式から各設問に及ぼす満足度への影響度は解釈できますが、切片の値 $7.0$ が何を表すのか解釈できません。そこで、さらに解釈しやすい式への変形を行います。
まず、各設問内のカテゴリ数量の平均が0となるように、以下の表のようにカテゴリ数量の変換を施します。このような処理を カテゴリ数量の基準化 と言います。また、切片は満足度(設問5)の平均点となります。
| カテゴリ | 度数 | 回帰係数 (カテゴリ数量) |
カテゴリ数量の平均 | カテゴリ数量の基準化 | |
| 設問1 | 十分 | 5 | 1.7 | 1.09
$\left(=\dfrac{5\times 1.7+3\times 1.2 + 3\times 1.4 +4 \times 0}{5+3+3+4}\right)$ |
0.61 (= 1.7 – 1.09) |
| 普通 | 3 | 1.2 | 0.59 (= 1.2 – 1.09) |
||
| やや不十分 | 3 | 1.4 | 0.79 (= 1.2 – 1.09) |
||
| 不十分 | 4 | 0 | -1.09 (= 0 – 1.09) |
||
| 設問2 | 多い | 4 | 1.4 | 0.41
$\left(=\dfrac{4\times 1.4+5\times 0.1 + 6 \times 0}{4+5+6}\right)$ |
0.99 (= 1.4 – 0.41) |
| 普通 | 5 | 0.1 | -0.31 (= 0.1 – 0.41) |
||
| 少ない | 6 | 0 | -0.41 (= 0 – 0.41) |
||
| 設問3 | 高い | 4 | -3.7 | -1.59
$\left(=\dfrac{4\times -3.7-6\times 1.5 + 5 \times 0}{4+6+5}\right)$ |
-2.11 (= -3.7 + 1.59) |
| 普通 | 6 | -1.5 | 0.09 (= -1.5 + 1.59) |
||
| 安い | 5 | 0 | 1.59 (= 0 + 1.59) |
||
| 設問4 | 早い | 6 | 0 | -0.29
$\left(=\dfrac{4\times 0+5\times -0.8 + 4 \times -3.0}{6+5+4}\right)$ |
0.29 (= 0 + 0.29) |
| 普通 | 5 | -0.8 | -0.51 (= -0.8 + 0.29) |
||
| 遅い | 4 | -3.0 | -0.01 (= -3.0 + 0.29) |
||
| 切片 | 7 | 6.55 (設問5の平均点) |
– |
よって、カテゴリ数量の基準値を用いると全体的な満足度の式は

と表されます。この式を用いることによって、全体的な満足度の平均値を基準(切片)にして、各設問の影響度を確認することができるようになります。


