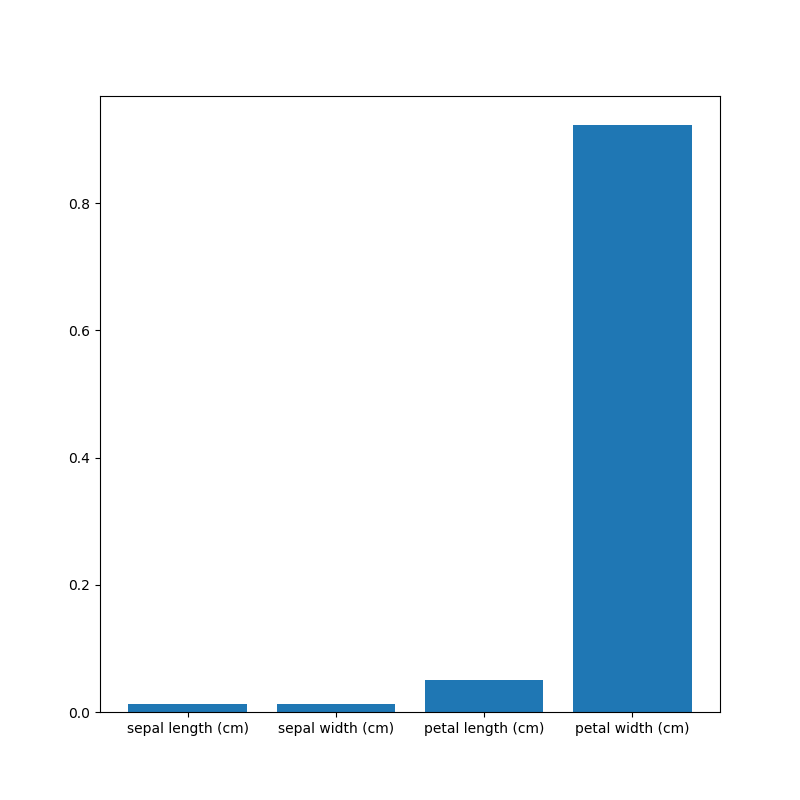
機械学習の手法は多く存在しており、
データの対象や目的によって、選定する必要があります。

製造業において不良を発見したい場合、「正常」「異常」の正解ラベルを付与し、
分類問題として考えても良いですが、
一般に、製造業における製品の不良率は1%未満であることが多く、
データセットの内訳として正常データと異常データが同数ではないケースが大半です。
そのような場合は「異常検知（外れ値検出）」の手法を用いるべきです。

Isolation Forestは異常検知のアルゴリズムの一種です。

異常検知手法①でお伝えしたLOFは密度分布に基づいており、
「疎であれば異常、密であれば正常」という考えで異常度を算出します。
Isolation Forestもその考えに基づきますが、
密度を算出するわけでなく、”空間分割の多さ”によって異常であるかを判断します。
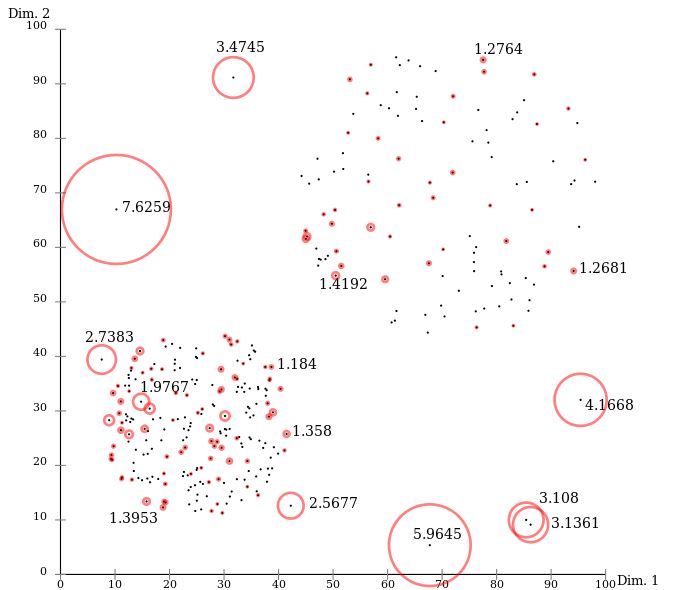
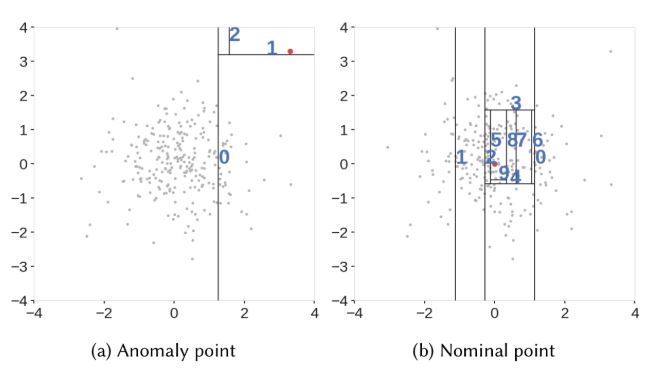
下図[1]は、ある2次元のデータに対してIsolation Forestを適用した例です。
Isolation Forestはサンプルデータ群の空間において、
１つの空間内に属するデータが規定の個数になるまで、分割を繰り返します。
結果的に同図(a)のような疎なデータの空間分割数は2に、
同図(b)のような密なデータの空間分割数は9となり、
差異が生じることがわかります。

LOFは密度の計算を行うために、近傍点を収集する計算処理コストが大きいですが、
Isolation Forestは空間分割法を使うことで、高速に処理することが可能です。

[1]…Hariri, Sahand; Carrasco Kind, Matias; Brunner, Robert J. (2019). “Extended Isolation Forest”. IEEE Transactions on Knowledge and Data Engineering　より抜粋

機械学習の手法は多く存在しており、
データの対象や目的によって、選定する必要があります。
　
　
製造業において不良を発見したい場合、「正常」「異常」の正解ラベルを付与し、
分類問題として考えても良いですが、
一般に、製造業における製品の不良率は1%未満であることが多く、
データセットの内訳として正常データと異常データが同数ではないケースが大半です。
そのような場合は「異常検知（外れ値検出）」の手法を用いるべきです。
　
　
LOF(Local Outlier Factor)は異常検知のアルゴリズムの一種です。
　
　
LOFは密度分布に基づいており、
「疎であれば異常、密であれば正常」という考えで異常度を算出します。
下図は、ある2次元のデータに対してLOFを適用し、異常度を算出した例です。
数値が高いデータは疎であることが分かります。
異常度は、1つのデータ(点)に対する近傍点群を収集し、
それらまでの距離や密度を計算することで算出します。

　　
　
欠点は以下です。
・疎密であることを利用しているため、データ数を多く必要とする。
・近傍点までの距離を1点ずつ計算するため、計算コストが高い。
　
欠点はありますが、アルゴリズムは単純であり、
分かりやすく、説明し易いです。
よって、手法のベンチマークでも良く見かけられる手法でもあります。

アンサンブル学習という手法群をご存じでしょうか？
平たく言うと、“多数決”によって最終的な結果を求める手法を指します。
ランダムフォレストは決定木のアンサンブル学習器として発明され、
一般に、決定木よりも精度が高くなることから、
実際によく使用されています。

 

■生成手順
ランダムフォレストのモデル生成手順を以下に示します。
１．学習データを用意する。
２．ブートストラップ法を用いて学習データを複数作成する。

　　同手法は内容の異なる複数の学習データを作成する手法です。
　　手順１で与えられた学習データから、
　　ランダムに復元抽出を行うことで作成します。

３．一部の特徴量をランダムに削除する。
４．手順３で得られた学習データから決定木を各々に作成する。

 

■予測方法
ランダムフォレストとは、生成手順４で得た複数の決定木そのものです。
実際に生成したモデルを用いて予測を行う場合は、
各予測対象データを各決定木に入力します。
各決定木の出力結果に対して多数決を行った結果が
ランダムフォレストの結果となります。

昨今、ディープラーニングが流行していますが、
今日時点の手法においては、欠点もあります。
実際にAIの適用を考える段階で、
“AIのモデルを生成した結果、何故、そのような分類結果となったのか？”を
説明することができないという点です。
このように、分類結果の根拠を説明できない手法群を“説明不可能なAI”と呼びます。

一方で、“説明可能なAI”の代表例として
決定木と呼ばれる手法が存在します。
本記事では同手法の概要を紹介します。

 

決定木は所謂、教師あり学習であり、
出力として予測精度および、
どのデータが重要であったかを示す重要度を
算出することが可能です。

試しに、下の散布図行列に示すirisデータを決定木で分類してみます。
散布図の結果から、pedal widthやlengthのデータに着目すれば
適切に分割できるように見受けられます。

次に、決定木でモデルを生成し、その構造を可視化しました。
・決定木は木構造を用いて空間を分割します。
・決定木は各分類ラベルを情報利得（図中の場合、”gini”の値）に基づいて分類をします。この値は、分類結果の各グループにおいて、ラベルが混在していない度合を定量的に示しています。この値が小さければ、綺麗に分類できていると言えます。

可視化結果を見ると、pedal widthやlengthを条件に、
枝を作っている箇所が木の根の近くに存在しており、
同データらが重要そうだと言えそうです。

さらに、重要度を可視化してみました。
値が高ければ重要であり、今回の分類事例においては、
全４種のデータのうちpedal widthが最も重要だと定量的に言えます。
このことは、上述の散布図から見受けた判断を裏付けることになり、
分類の根拠と言えます。

決定木はディープラーニングにはできない、上述のような根拠を提示することが可能です。ディープラーニングと比べると、精度は劣りますが、スモールスタートで妥当性を確認したい場合などは有効な手法だと言えます。