AとBに正の相関があり、AとCに正の相関がある場合に、本来は関係のないBとCにも正の相関があるように見えてしまう場合があります。

例えば、

$~~~$A：気温　、B：アイスクリームの売上　、C：扇風機の販売台数

として、それぞれ散布図を書くと以下のような結果になったとします。
(値は適当です。)

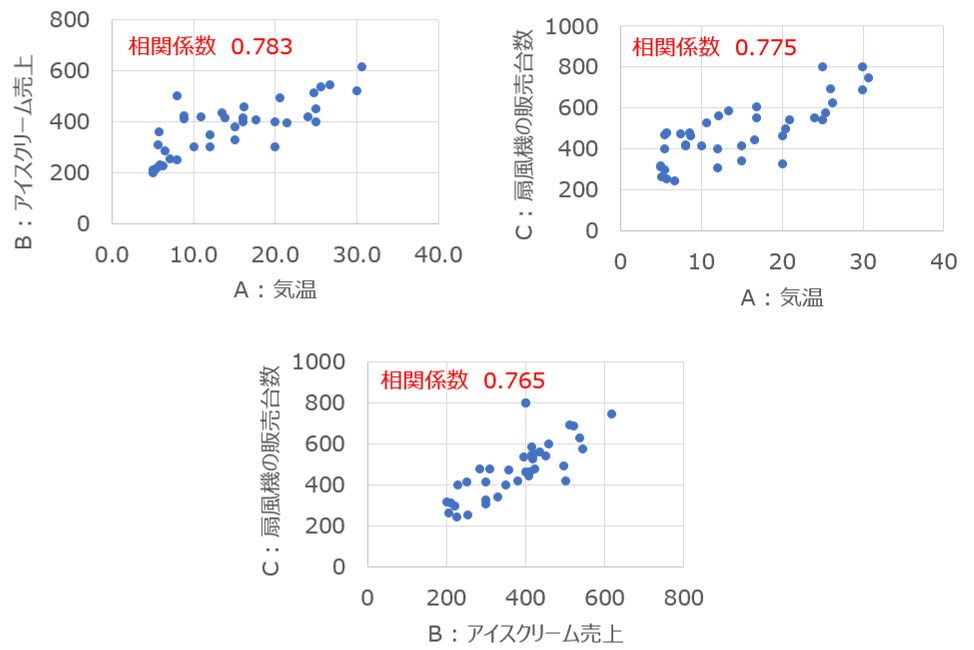
一般論的として、

$~~~~$気温 が高いほど、アイスクリーム が売れる
$~~~~$気温 が高いほど、扇風機の販売台数 が増える

ことは考えられますが、

$~~~~$アイスクリームの売上 と 扇風機の販売台数

の間には直接的な関係性はないはずです。しかしながら、0.765という高い相関が得られています。

このように共通原因(ここでは気温)をもったために本来相関がないであろう変数間に相関がみられることを、見かけ上の相関 や 擬似相関 といいます。
 
　擬似相関が疑われるような場合には、偏相関係数 と呼ばれるものを計算します。

偏相関係数とは、今回の例では、「A:気温 の影響を除いた B:アイスクリームの売上」と「A:気温 の影響を除いた C:扇風機の販売台数」の相関係数のことを言い、

式で表すと、
\begin{align*}
偏相関係数= \dfrac{\rho^{~}_{BC}-\rho^{~}_{AB} \rho^{~}_{AC}}{\sqrt{1-\rho_{AB}^{2}} \sqrt{1-\rho_{AC}^{2}}}
\end{align*}
から計算されます。($\rho^{~}_{XY}$の表記は　$X$ と $Y$ の相関を表す)

 

「B：アイスクリームの売上」 と 「C：扇風機の販売台数」 に関して偏相関係数を計算すると、偏相関係数は0.403となり、やはりBとCには関係性はないと判断することができます。