ベイズ統計学 では 一般的な統計学 とは前提の考え方が異なっています。
両者を比較してみましょう。

一般的な統計学では、得られた観測データというのは、唯一の真の確率分布から、ランダムに抽出されたものであると考えます。仮に、真の確率分布が正規分布であるとするならば、平均・分散は定数であり、非確率変数になります。

 

 

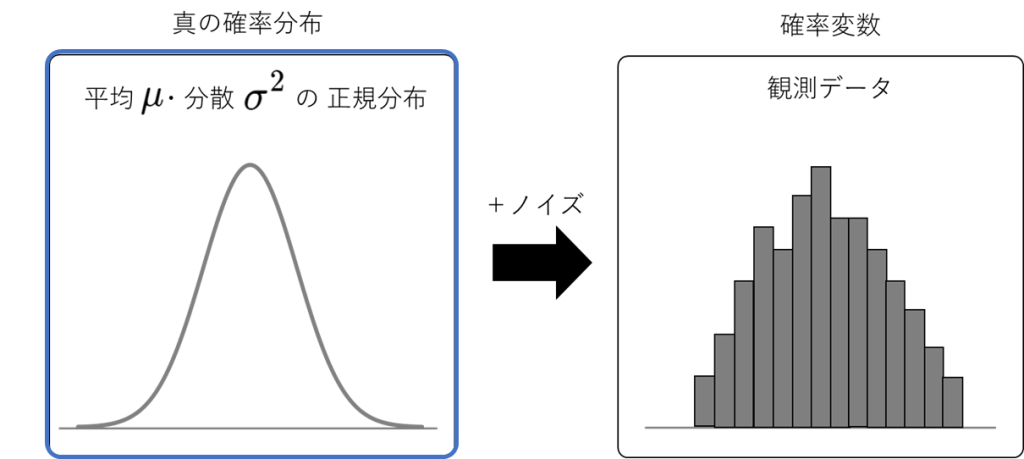
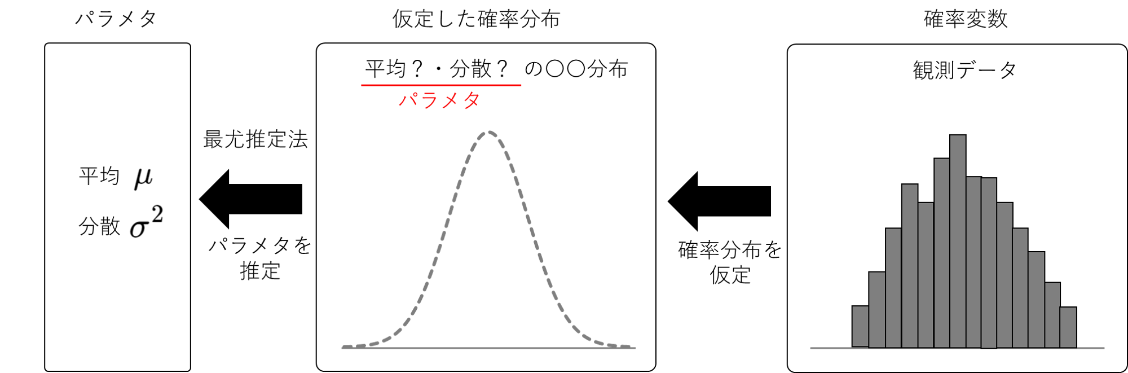
そのため、一般的な統計学では、得られた観測データから、背景にある確率分布を仮定し、ある定数である平均と分散を推定することが最終目標になります。

 

 

 

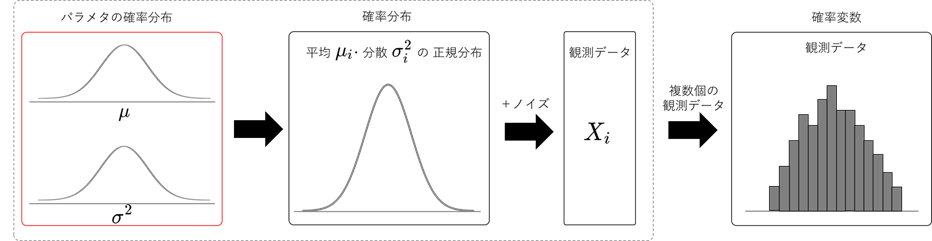
一方、ベイズ統計学では、背景に唯一の真の確率分布があるとは考えずに、真の確率分布は変化するものであると考えます。得られた観測データというのは、毎回異なる確率分布から、ランダムに抽出されたものであると考えます。仮に、背景の確率分布を正規分布であると仮定するならば、平均、分散が変数となり、確率変数になります。

 

 

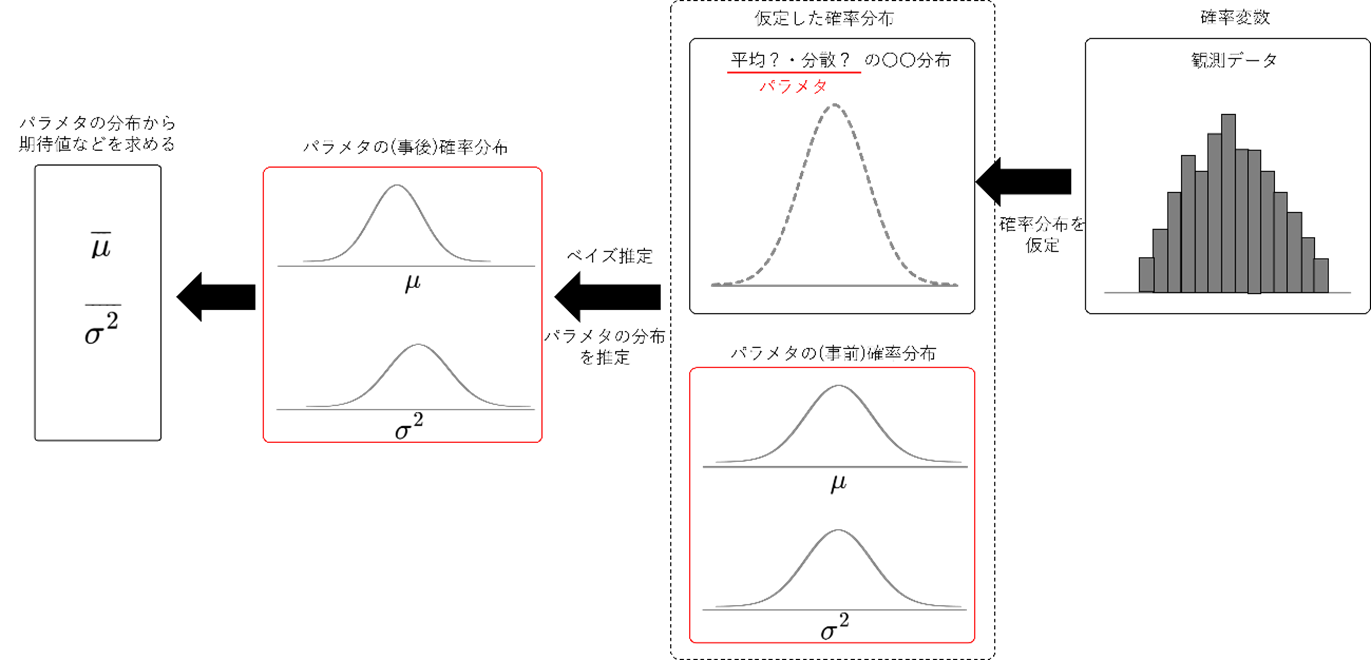
そのため、ベイズ統計学では、得られた観測データから、背景にある確率分布を仮定し、平均・分散の確率分布を求めることが最終目標になります。

 

 

(ベイズ統計学を用いるメリット)

ベイズ統計学を用いるメリットは平均・分散といったパラメタの確率分布を求められる点にあります。

 

例えば、実験Aと実験Bの平均値に差があるか？という問題があったとします。

 

一般的な統計学では、帰無・対立仮説、有意水準を設定し、検定統計量と有意水準の大きさを比較して・・・、ということを行いますが、ベイズ統計学では、差の確率分布を直接求めることができます。

   |実験Aの平均 – 実験Bの平均|>0 である確率は〇〇％。

   (実験Aの平均 – 実験Bの平均)＞0 である確率は△△％

といったように、非常に直感的に解釈がしやすい結果を得ることが可能になります。これが、ベイズ統計学を用いるメリットの1つになります。

 

ベイズ統計学のもう1つのメリットは、事前にパラメタの確率分布の知識を持っていれば、少数のデータでもある程度の精度を保った推定が行えることにあります。

 

(ベイズ統計学のデメリット)

ベイズ統計学を扱うためには、MCMC（マルコフ連鎖モンテカルロ法）という乱数生成アルゴリズムを用いる必要があります。プログラミングを行う必要があるため、初学者が気軽に扱えないという点がデメリットになります。