AとBには “相関がある”、”相関がない” という言葉を聞いたことがある方は多いのではないでしょうか？2つの値の相関の強さを表す指標を 相関係数 といいますが、ひとえに “相関係数” といっても、

$~~~~~$「(ピアソンの)積率相関係数」、「順位相関係数」、
$~~~~~$「偏相関係数」、「自己相関係数」など

様々な相関係数が存在します。単に相関係数と呼ぶ場合には、通常は「(ピアソンの)積率相関係数」をさしています。

今回は、「(ピアソンの)積率相関係数」、「順位相関係数」について解説します。

 

「積率相関係数」について

　データがともに量的変数 である場合に用いられる相関係数です。

例えば、”体重と身長” の関係や、”駅からの距離と家賃”、”年齢と血圧” など両者ともに定量的な値を持つ場合に活用されます。

相関があるとは2つのデータ間に直線的な関係があることを意味します。

$~~~~~$Aが大きくなるとBも大きくなる場合には 正の相関 がある
$~~~~~$Aが大きくなるとBが小さくなる場合には 負の相関 がある

といいます。

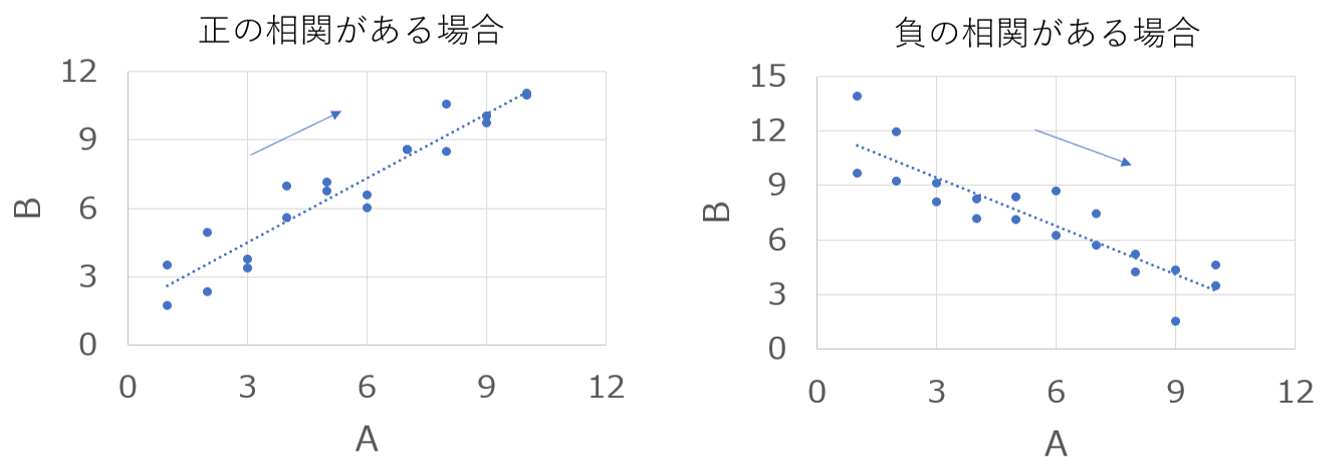
ただし、以下のようなデータの場合にはAとBには明らかに関係性がありそうですが、直線では表せないため相関はないと判断されます。

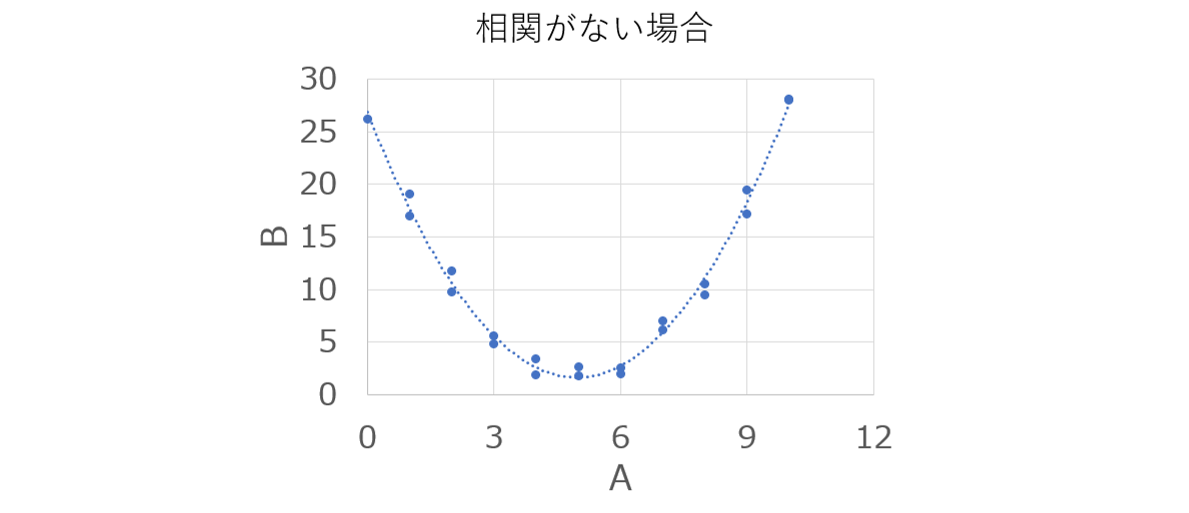
このように、相関がないことは、因果関係がないことを示すわけではないため、あくまで相関は1つの指標であり、値を図にプロットして確認することが非常に重要になります。

 

「順位相関係数」について

　データがともに質的変数で、順位である場合に用いられる相関係数です。

例えば、”男女の好きな果物の順位” の関係や、”去年と今年の月別降水量の順位”、 など順位で表せる場合に両者の関係性をはかる手段として活用されます。

順位相関係数の求め方として

「スピアマンの順位相関係数」「ケンドールの順位相関係数」

が良く使われるそうです。順位相関係数には複数の求め方があり、目的に応じて順位相関係数の算出方法を決める必要があるということを覚えておけばよいかと思います。