(例題)

　1日当たりの来店者数を1年間調査したところ、以下のような度数分布が得られたとします。この度数分布から、平均値・中央値の信頼区間を求めてみます。

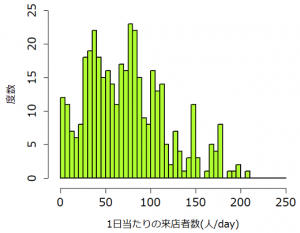
(問題点)
　①上記の度数分布では、どのような確率分布を仮定するべきなのかわからない。
　②中央値の信頼区間を求める解析的に解く方法がない。

   

(ブートストラップ法)
　このような問題の対処法の一つに、数値解析的に解く ブートストラップ法が用いられます。

ブートストラップ法は、“標本の分布は母集団の分布を再現している” という 仮定 のもと、標本の分布から復元抽出を行い、復元抽出した標本のデータをもとに 母集団の分布を推測 する方法です。

ブートストラップ法は以下の手順を踏みます。標本データ数を$n$とすると、
① $n$個の標本データから、新たに $n$ 個のデータを復元抽出する。
(ブートストラップ標本とよばれます)
② ブートストラップ標本の平均値・標準偏差・中央値を算出する。
③ ①と②を $B$ 回繰り返す。(今回は、$B=10000$ としました)
④ $B$ 回の繰り返しにより得られた平均・標準偏差・中央値の度数分布を確認する。
⑤ ④で得られた度数分布を元に区間推定を行う

   

(平均値の信頼区間)
　上記例において、ブートストラップ法の手順④まで計算を行うと、平均値の累積度数は以下のように得られました。

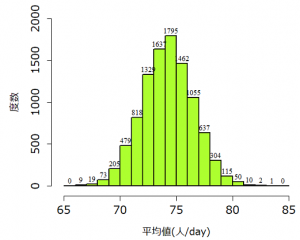
この結果から、例えば、”平均値 ≦$71$”となる確率は
\begin{align*}
(9+19+73+209+479)/10000 =0.079
\end{align*}
であり、”平均値 ≧ $79$” となる確率は
\begin{align*}
(1+2+10+50+115+304)/10000= 0.049
\end{align*}
なので、母集団の平均値のおおよその90％信頼区間は、
\begin{align*}
71 < 平均値 < 79
\end{align*}
と求められます。

   

(中央値の信頼区間)
　同様に、中央値の累積度数は以下のように得られました。

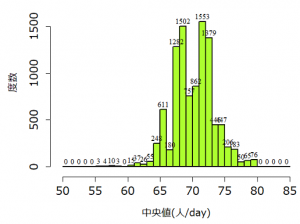
この結果から、例えば、中央値 ≦$65$ となる確率は
\begin{align*}
\dfrac{3+4+10+3+15+37+26+55+248}{10000} =0.040
\end{align*}
であり、 中央値 ≧ $76$ となる確率は
\begin{align*}
\dfrac{76+65+50+183+206}{10000}= 0.058
\end{align*}
なので、母集団の中央値のおおよその90％信頼区間は、
\begin{align*}
65 < 中央値 < 76
\end{align*}
と求められます。