(回帰分析)
回帰分析とは、”原因”と”結果”の関係を定量的に表すための手法です。
($X_{1} , Y_{1}$) , ($X_{2} , Y_{2}$) ,$\cdots$ , ($X_{n} , Y_{n}$) というデータがあるときに、
Y=aX+b
\end{align*}
のように $X$ と $Y$ の関係を定量的に表す手法です。$Y$ は目的変数(従属変数)、$X$ は説明変数(独立変数)などと呼ばれます。
例えば、以下のように各営業所における販売員の人数(説明変数)と売上(目的変数)のデータがあったとします。
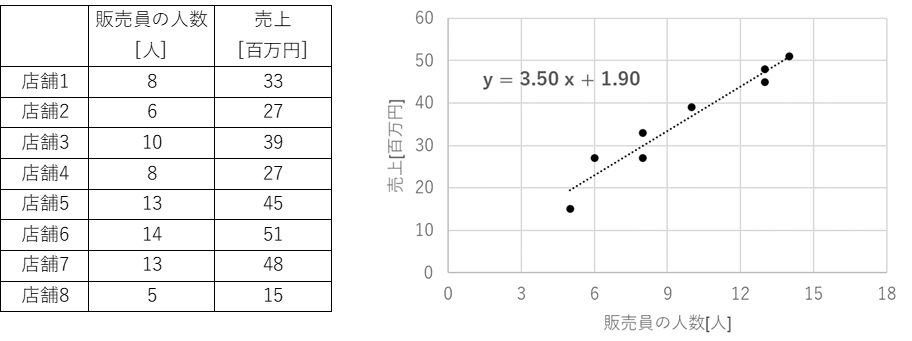
このデータを回帰分析してみると、
「売上 = 3.5 × 販売員の人数 + 1.90 」
という関係式が得られ、販売員の人数(説明変数)を1人増やせば、売上(目的変数)は約3.5[百万円]増加することが推定することができます。
上記の例では、売上に影響する説明変数が 販売員の人数の1つだけでしたが、他にも様々な説明変数が売上に影響することが想定されるでしょう。回帰分析でも、説明変数が1つの場合には単回帰分析、説明変数が2つ以上ある場合には重回帰分析と呼ばれています。
Y=a_{1}X_{1}+a_{2}X_{2}+\cdots + b
\end{align*}
(重要度)
それでは、売上に影響する説明変数を1つ追加し、販売員の人数[人]、広告費[千万]の2つが説明変数であるとします。
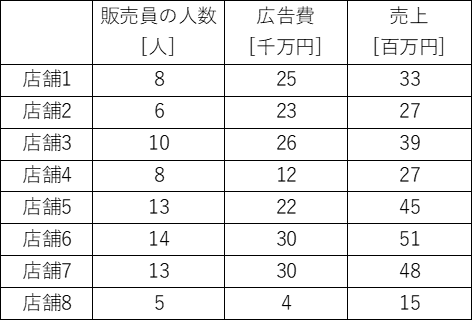
これらのデータを重回帰分析すると、
「売上=2.6 × 販売員の人数 + 0.48 × 広告費 + 0.31 」
という結果が得られます。
このとき、売上により影響するのは、販売員の人数と広告費のどちらと言えるでしょうか?単純に係数(2.6と0.48)の大きさの比較から、“販売員の人数”と答えたくなるかもしれませんが、この係数比較では適切には判断することができません。なぜなら係数の単位がそれぞれ、3.5[百万円/人]、0.5[百万円/千万円]と異なっているからです。
このような問題に対して、回帰分析を行う前には、データのスケール(単位)を統一するという前処理を行います。
(データの標準化)
$~~~~~$データ $X$ の平均が $\bar{X}$ 、標準偏差 $\sigma$ であるとき、そのデータを
\dfrac{X-\bar{X}}{\sigma}
\end{align*}
と変換します。この変換を 標準化 といいます。標準化により、単位は無次元に統一され、分布 は 平均0、分散1 に統一されます。
例えば、販売員の人数の標準化は、
「ある営業所の販売員の人数 – 販売員の人数の平均 / 販売員の人数の標準偏差」
という計算をそれぞれのデータに対して行います。

同様に広告費に関しても標準化を行い、データのスケール(単位)を無次元に揃えてから、回帰分析を実施することによって、
売上[百万円]=8.9[百万円] × 標準化した販売員の人数(無次元)
+ 4.3[百万円] × 標準化した広告費(無次元) + 35.6[百万円]
という式が得られるようになります。この結果から、誰が見ても広告費よりも販売員の人数の方が売上への影響度が大きいことが明らかになります。


