投稿日:

主成分分析を図を使ってイメージする

　主成分分析とは、「データの次元を削減し、データの特徴を捉えやすくするために用いられる手法」です。主成分分析のイメージを図から感覚的に捉えてみましょう。

   

　図示可能な3次元データを例として用います。以下のような3次元データが得られたとします。


この3次元データを違う方向から見ると、ある平面上付近にデータが集まっていることがわかります。

よって、この平面上に新たな2軸を作成すると、今回の3次元のデータは2次元データとして捉えることが可能となります。

すべてのデータが平面上にはないので、平面に対して垂直方向のずれ(情報)は捨てることになりますが、

“平面上付近にデータが分布する”というデータの大きな特徴は捉えることができています。(主成分分析では、元のデータの80～90％の情報は残るように次元を調整します。)

このように、主成分分析では、新たな軸を設けて、次元を削減することによって、データの特徴をより簡略的に捉えることが可能となります。

投稿日:

確率分布の特定が困難な場合の区間推定方法


(例題)

　1日当たりの来店者数を1年間調査したところ、以下のような度数分布が得られたとします。この度数分布から、平均値・中央値の信頼区間を求めてみます。


(問題点)
　①上記の度数分布では、どのような確率分布を仮定するべきなのかわからない。
　②中央値の信頼区間を求める解析的に解く方法がない。

   

(ブートストラップ法)
　このような問題の対処法の一つに、数値解析的に解く ブートストラップ法が用いられます。

ブートストラップ法は、“標本の分布は母集団の分布を再現している” という 仮定 のもと、標本の分布から復元抽出を行い、復元抽出した標本のデータをもとに 母集団の分布を推測 する方法です。

ブートストラップ法は以下の手順を踏みます。標本データ数を$n$とすると、
① $n$個の標本データから、新たに $n$ 個のデータを復元抽出する。
(ブートストラップ標本とよばれます)
② ブートストラップ標本の平均値・標準偏差・中央値を算出する。
③ ①と②を $B$ 回繰り返す。(今回は、$B=10000$ としました)
④ $B$ 回の繰り返しにより得られた平均・標準偏差・中央値の度数分布を確認する。
⑤ ④で得られた度数分布を元に区間推定を行う

   

(平均値の信頼区間)
　上記例において、ブートストラップ法の手順④まで計算を行うと、平均値の累積度数は以下のように得られました。

この結果から、例えば、”平均値 ≦$71$”となる確率は
\begin{align*}
(9+19+73+209+479)/10000 =0.079
\end{align*}
であり、”平均値 ≧ $79$” となる確率は
\begin{align*}
(1+2+10+50+115+304)/10000= 0.049
\end{align*}
なので、母集団の平均値のおおよその90％信頼区間は、
\begin{align*}
71 < 平均値 < 79
\end{align*}
と求められます。

   

(中央値の信頼区間)
　同様に、中央値の累積度数は以下のように得られました。

この結果から、例えば、中央値 ≦$65$ となる確率は
\begin{align*}
\dfrac{3+4+10+3+15+37+26+55+248}{10000} =0.040
\end{align*}
であり、 中央値 ≧ $76$ となる確率は
\begin{align*}
\dfrac{76+65+50+183+206}{10000}= 0.058
\end{align*}
なので、母集団の中央値のおおよその90％信頼区間は、
\begin{align*}
65 < 中央値 < 76
\end{align*}
と求められます。

投稿日:

新たなサンプルを抜きとったときの予測値


(新たなに抜き取ったりんごの重さは？)

   前回の記事では、あるりんご園からりんご 5個 をサンプリングした結果、その重さ $(\mathrm{g})$ がそれぞれ、
\begin{align*}
288&&292&&305&&298&&290
\end{align*}であった場合に、標本平均 $\overline{X}(=295)$ から、母集団の平均値を推定 する方法について述べました。

 

   しかし、例えば、出荷できるりんごの重さの範囲が決められているような場合には、知りたいのは平均値ではなく、新たなサンプル のリンゴを1個 抜き取った ときに、そのリンゴの重さが

$~~~~~~~~$1. $~~300\,\pm5$ の範囲にある 確率 はいくらか？
$~~~~~~~~$2.「$99.9$% の確率でこの 範囲 に入る」と言えるのは、$295\,\pm$ いくらか？

ということになります。ここでは、この疑問に対する答えを考えていきます。

 

(理論的な背景)

   新たなリンゴのサンプルを確率変数 $X$ と表します。前回の記事では、確率変数 $X$ の 期待値 $E(X)$ および 分散 $V(X)$ が、
\begin{align*}
E(X)=\mu\,,&&V(X)=\sigma^2
\end{align*}であるとき、その平均 $\overline{X}$ の 期待値 $E(\overline{X})$ および 分散 $V(\overline{X})$ は
\begin{align*}
E(\overline{X})&=\mu~,\\[6pt]
V(\overline{X})&=\frac{\sigma^2}{n}
\end{align*}となることを示しました。

 

   そこで、次に、確率変数 $X-\overline{X}$ について考えます。$X$ と $\overline{X}$ は独立なので、その期待値は
\begin{align*}
E(X-\overline{X})=E(X)-E(\overline{X})=\mu-\mu=0,
\end{align*}分散は、
\begin{align*}
V(X-\overline{X})=V(X)+V(\overline{X})=\sigma^2+\frac{\sigma^2}{n}=\left(1+\frac{1}{n}\right)\sigma^2
\end{align*}となります。つまり、確率変数
\begin{align*}
Z=\frac{X-\overline{X}}{\sqrt{\left(1+\dfrac{1}{n}\right)\sigma^2}}
\end{align*}は標準正規分布 $\mathrm{N}\left(0,1^2\right)$ に従います。決まった値である分散 $\sigma^2$ の代わりに、分布をもった推定量である不偏分散  $s^2$ を用いたとき、確率変数
\begin{align*}
t=\frac{X-\overline{X}}{\sqrt{\left(1+\dfrac{1}{n}\right)s^2}}
\end{align*}の分布は 自由度 $n-1$ の $t$ 分布 となることが知られています。

 

(6個目のリンゴの重さを予測する)

   初めの例 $(n=5)$
\begin{align*}
288&&292&&305&&298&&290
\end{align*}でいえば、
\begin{align*}
t=\frac{X-295}{\sqrt{\dfrac{6}{5}}\times 6.67}
\end{align*}であり、$X=295, 305$ に相当する $t$ はそれぞれ $t = 0 , 1.37$ であるから、自由度 $4$ の $t$ 分布を調べて、
\begin{align*}
&P\left(X< 295\right)=P\left(t< 0\right)=0.5~,\\[6pt]
&P\left(X> 305\right)=P\left(t> 1.37\right)=0.12~,\\[6pt]
\end{align*}となるので、新たに抜き取った 6 個目のリンゴ $X$ が $300 \pm 5$ に入る確率は
\begin{align*}
1-(P\left(X< 295\right)+P\left(X> 305\right))=0.378,
\end{align*}つまり、$37.8$% であると求められます。

投稿日:

標本平均から母平均を推定する

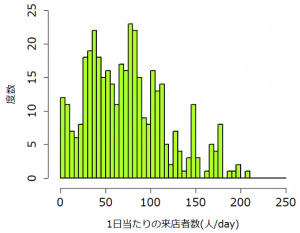
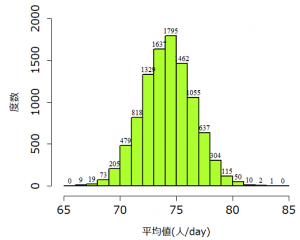
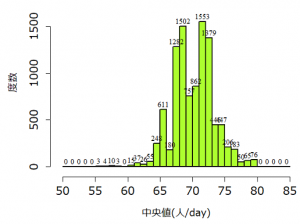
(標本平均)

   例えば、あるりんご園からりんご 5 個 をサンプリングした結果、そのりんごの重さ $(\mathrm{g})$ がそれぞれ、

\begin{align*}
288&&292&&305&&298&&290
\end{align*}

であったとします。標本の平均値は、

\begin{align*}
\overline{X}=\frac{288+293+305+298+291}{5}=295
\end{align*}

となりますが、これは母集団の平均ではありません。

 

今回たまたま得られた標本の平均値から、母集団の平均値が

$~~~~~~~~$1. $~~300\,\pm5$ の範囲にある 確率 はいくらか？
$~~~~~~~~$2.「$99.9$% の確率でこの 範囲 に入る」と言えるのは、$295\,\pm$ いくらか？

のような疑問に対する答えを考えていきましょう。

 

(間違い例)

   不偏分散 $s^2$ は、

\begin{align*}
s^2=\frac{1}{n-1}\sum_{i=1}^n\left(X_i-\overline{X}\right)^2
\end{align*}

によって求められる、母集団の 分散 $\sigma^2$ の 推定値 になります。上の例でいえば、

\begin{align*}
s^2=\frac{(288-295)^2+\cdots+(291-295)^2}{5-1}=44.5
\end{align*}

になります。

$s=\sqrt{44.5}\approx 6.67$ なので、正規分布と見なして、$295 \pm 3s=295\pm20$ の範囲に $99.7$% の確率で入るだろう、ということはやってはいけません。

 

(確率変数の変換)

   確率変数 $X$ の 期待値 $E(X)$ および 分散 $V(X)$ が、

\begin{align*}
E(X)=\mu\,,&&V(X)=\sigma^2
\end{align*}

であるとき、定数 $a,b$ によって $X$ からつくられた確率変数 $Y=aX+b$ は、

\begin{align*}
E(Y)=a\mu+b\,,&&V(Y)=a^2\sigma^2
\end{align*}

という性質を持ちます。いま、確率変数 $X$ が、正規分布 $\mathrm{N}\left(\mu,\sigma^2\right)$ に従うとき、

\begin{align*}
Z=\frac{X-\mu}{\sigma}
\end{align*}

は、標準正規分布 $\mathrm{N}\left(0,1^2\right)$ に従います。

同様に、

\begin{align*}
\overline{X}=\frac{X_1+X_2+\cdots+X_n}{n}
\end{align*}

は、$X_1,X_2,\cdots,X_n$ が独立であることから、

\begin{align*}
E(\overline{X})&=\frac{E(X_1)}{n}+\frac{E(X_2)}{n}+\cdots+\frac{E(X_n)}{n}=n\cdot\frac{\mu}{n}=\mu~,\\[6pt]
V(\overline{X})&=\frac{V(X_1)}{n^2}+\frac{V(X_2)}{n^2}+\cdots+\frac{V(X_n)}{n^2}=n\cdot\frac{\sigma^2}{n^2}=\frac{\sigma^2}{n}
\end{align*}

が成り立ち、$\overline{X}$ は正規分布 $\mathrm{N}\left(\mu,\sigma^2/n\right)$ に従いますので、

\begin{align*}
Z=\frac{\overline{X}-\mu}{\sqrt{\dfrac{\sigma^2}{n}}}
\end{align*}

は、標準正規分布 $\mathrm{N}\left(0,1^2\right)$ に従います。

 

(カイ二乗分布)

   上述の 分散 $\sigma^2$ は、ある 決まった値 です。これに対して、私たちが用いようとしている 不偏分散 $s^2$ は、

\begin{align*}
E\left(s^2\right)=\sigma^2
\end{align*}

ではあるものの、推定値 であり、分布 をもっています。

この $\dfrac{n\cdot s^2}{\sigma^2}$ の分布を、自由度 $n-1$（図中の $k$）の $\chi^2$ 分布 (カイ二乗分布)と呼びます。

 

($t$ 分布)

   では、

\begin{align*}
Z=\frac{\overline{X}-\mu}{\sqrt{\dfrac{\sigma^2}{n}}}
\end{align*}

の $\sigma^2$ の代わりに、分布をもった $s^2$ を用いた

\begin{align*}
t=\frac{\overline{X}-\mu}{\sqrt{\dfrac{s^2}{n}}}
\end{align*}

はどのような分布となるのでしょうか。

この分布を Student（発表者のペンネーム）の $t$ 分布 と呼びます。$t$ 分布の自由度 $\nu$ は、$\nu=n-1$ となります。

 

(母平均の推定)

   例えば、初めの例 $(n=5)$

\begin{align*}
288&&292&&305&&298&&290
\end{align*}

でいえば、

\begin{align*}
t=\frac{295-\mu}{\dfrac{6.67}{\sqrt{5}}}
\end{align*}

であり、$\mu=295, 305$ に相当する $t$ はそれぞれ $t=0,-0.67$ であるから、自由度 $4$ の $t$ 分布を調べて、

\begin{align*}
&P\left(\mu \lt 295 \right) = P \left(t \gt 0\right)=0.50~,\\
&P\left(\mu \gt 305 \right)=P\left(t \lt -0.67\right)=0.270
\end{align*}

なので、母集団の 平均値 $\mu$ が $300\pm5$ にある確率は

\begin{align*}
1-\left((P\left(\mu \lt 295 \right)+P\left(\mu \gt 305 \right)\right) =0.33,
\end{align*}

つまり、 $33.0$% と求めることができます。

 

投稿日:

回帰分析結果に付随するt値について

   SPSSやEXCEL、R等を用いて回帰分析を行うと、回帰係数の値だけではなく、結果の妥当性を判断するための指標である 「$t$ 値」 (または「$t$」と表示)と呼ばれる結果が必ず付随します。今回は、この「$t$ 値」の意味について解説します。回帰分析、検定については、前回の記事を参照ください。

 

(回帰係数も確率分布に従う)

   回帰分析 を1回行うと、ある1つの 回帰係数 の値が得られます。しかし、これは分析に用いたデータから “たまたま” 得られた結果です。実際には、①データ数 や ②データのばらつき により、回帰係数は “様々な” 値 をとります。そのため、回帰係数がとり得る値は①・②から決まる確率分布になっています。この分布は、$t$ 分布 と呼ばれる確率分布に従うことが知られており、$t$ 分布の $x$ 軸の値が $t$ 値と呼ばれています。

 

(回帰係数の値がゼロの可能性を否定できるか)

   回帰係数が “様々な” 値をとるということは、回帰係数がゼロである可能性 も否定できません。回帰係数がゼロである可能性を否定できない場合には、その説明変数に意味がない可能性があるため、一般的には、その説明変数を除外します。つまり、重回帰式

\begin{align*}
y=a_{1}x_{1}+a_{2}x_{2}+a_{3}x_{3}
\end{align*}

を例にすると、回帰係数 $a_{1}=0$ である可能性がある場合、その説明変数 $x_{1}$ は目的変数 $y$ を説明する変数となってない可能性があるため、説明変数 $x_{1}$ を回帰式から除外し、

\begin{align*}
y=a_{2}x_{2}+a_{3}x_{3}
\end{align*}

という式に修正することがあります。


(判断基準)

   回帰分析の結果得られる $t$ 値 は、その回帰係数が “ゼロではない確率” を間接的に表したものになります。実際の確率は、$t$ 分布から求められ、その確率は 有意確率 (P値) と呼ばれます。よく用いられるざっくりとした判定基準に、$t$ 値 の 絶対値が2以上、つまり、確率にして約 $95$% 以上 ある場合、回帰係数はゼロではない (例えば、$a_{1} \neq 0$)と判断し、その説明変数(例えば $x_{1}$) は目的変数を説明する変数として意味があると判断する、というものがあります。(実際には $t$ 値と確率の関係は、データのサンプル数によって変動します。$t$ 分布表を参照ください。)

投稿日:

仮説検定と有意水準

(仮説検定とは)

   仮説検定 とは、ある仮説を設けたときに、その仮説が正しいという前提のもとで、観測した結果が発生する確率を計算し、その 確率の大きさ から仮説の 正否を判断 する方法です。

例えば、コインを6回投げて、表が1回も出なかったとします。歪のないコイン (確率 $p = 1/2 $ ) であることを仮説とすると、この結果が得られる確率は、\begin{align*}
p^{6}=0.0156
\end{align*}ですので、仮説からすれば、表が1回も出なかったことは “稀”な、かなりずれた値となっています。よって、歪のないコインという 仮説は「誤っている」と判断されます。このとき仮説は「棄却される」といいます。

 

(有意確率(p値)とは)

   仮説が正しいという前提のもとで、観測した結果が発生する確率 のことを 有意確率(p値) といいます。上記のコインの例でいれば、有意確率(p値)は0.0156 ということになります。有意確率(p値)が小さいほど”稀”であるので、仮説は棄却されやすくなります。

 

(有意水準とは)

   上記のコインの例では、有意確率 0.0156 を勝手に”稀”と判断しましたが、あらかじめ “稀”と見なす基準を定める 必要があります。その 基準の確率を 有意水準 といいます。

 

・有意水準を0.05とした場合

   有意確率 (0.0156)  <  有意水準(0.05) なので 、 “稀” と判断され、仮説は棄却 されます。

このときの結論は、「歪のあるコインである」になります。

 

・有意水準を0.01とした場合

   有意確率 (0.0156)  >  有意水準(0.01) なので、“あってもおかしくない” と判断され、仮説は棄却されません。

このときの結論は、「歪のないコインかどうかはわからない」になります。

 

仮説が棄却されないことが、歪のないコインであるという仮説が真であることを直接的に証明したことにはなっていないことには注意が必要です。

投稿日:

回帰分析と標準化


(回帰分析)

   回帰分析とは、”原因”と”結果”の関係を定量的に表すための手法です。
($X_{1} , Y_{1}$) , ($X_{2} , Y_{2}$) ,$\cdots$ , ($X_{n} , Y_{n}$) というデータがあるときに、

\begin{align*}
Y=aX+b
\end{align*}

のように $X$ と $Y$ の関係を定量的に表す手法です。$Y$ は目的変数(従属変数)、$X$ は説明変数(独立変数)などと呼ばれます。

例えば、以下のように各営業所における販売員の人数(説明変数)と売上(目的変数)のデータがあったとします。
 

 
このデータを回帰分析してみると、
　　「売上 = 3.5 × 販売員の人数 + 1.90 」
という関係式が得られ、販売員の人数(説明変数)を1人増やせば、売上(目的変数)は約3.5[百万円]増加することが推定することができます。

 
上記の例では、売上に影響する説明変数が 販売員の人数の1つだけでしたが、他にも様々な説明変数が売上に影響することが想定されるでしょう。回帰分析でも、説明変数が1つの場合には単回帰分析、説明変数が2つ以上ある場合には重回帰分析と呼ばれています。

\begin{align*}
Y=a_{1}X_{1}+a_{2}X_{2}+\cdots + b
\end{align*}

 
(重要度)

　それでは、売上に影響する説明変数を1つ追加し、販売員の人数[人]、広告費[千万]の2つが説明変数であるとします。
 

 
これらのデータを重回帰分析すると、
　　「売上＝2.6 × 販売員の人数 + 0.48 × 広告費 + 0.31 」
という結果が得られます。
 
このとき、売上により影響するのは、販売員の人数と広告費のどちらと言えるでしょうか？単純に係数(2.6と0.48)の大きさの比較から、“販売員の人数”と答えたくなるかもしれませんが、この係数比較では適切には判断することができません。なぜなら係数の単位がそれぞれ、3.5[百万円/人]、0.5[百万円/千万円]と異なっているからです。
このような問題に対して、回帰分析を行う前には、データのスケール(単位)を統一するという前処理を行います。

(データの標準化)
$~~~~~$データ $X$ の平均が $\bar{X}$ 、標準偏差 $\sigma$ であるとき、そのデータを

\begin{align*}
\dfrac{X-\bar{X}}{\sigma}
\end{align*}

と変換します。この変換を 標準化 といいます。標準化により、単位は無次元に統一され、分布 は 平均0、分散1 に統一されます。

例えば、販売員の人数の標準化は、
「ある営業所の販売員の人数 – 販売員の人数の平均 / 販売員の人数の標準偏差」
という計算をそれぞれのデータに対して行います。

同様に広告費に関しても標準化を行い、データのスケール(単位)を無次元に揃えてから、回帰分析を実施することによって、

　　売上[百万円]＝8.9[百万円] × 標準化した販売員の人数(無次元)
　　　　　　　　　　　+ 4.3[百万円] × 標準化した広告費(無次元) + 35.6[百万円]

という式が得られるようになります。この結果から、誰が見ても広告費よりも販売員の人数の方が売上への影響度が大きいことが明らかになります。

投稿日:

統計解析を身近に！

今、「京都ビジネスアナライズのデータ分析サービス」始まりました。
顧客の立場で、「データを分析」「データ収集機能を開発」
「改善へのご支援」等、ＡＩを活用した新しいサポートでスタートしました。
お気軽にご相談してください。